Seite 5 von 5
Re: Aufgabe 20 (K)
Verfasst: Mi 26. Nov 2008, 12:29
von pedobear
mocha hat geschrieben:
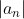
ist doch
größer gleich
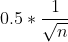
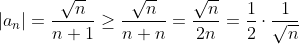
und deswegen ist
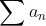
nicht absolut konvergent
weil
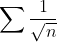
divergiert und damit auch
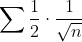
oder was mach ich falsch

gleich am anfang ziehst du den betrag von an und machst den Bruch dann größer, am ende sagste dann yo und wegen minoranten etc...
das Minorantenkriterium besagt aber das wenn 0 <= bn <= an , nich wenn 0 <= bn <= |an|.
durch den betrag "klappste" ja einfach alle glieder über die x Achse un sagst dann yo das divergiert.
da aber eigentlich manche Glieder unter der x Achse sind, ist die summe von an ja westenlich kleiner als die von |an|, in dem Fall so stark das das an evtl nicht mehr divergiert !
nimm dir z.bsp. an= (-1)^n * 1/n
|an| = 1/n, das divergiert ja an sich.
so jetz lass die betragstriche weg... zackbumm nix mehr mit divergenz, alle glieder von sn sind kleiner gleich 1 :/
Re: Aufgabe 20 (K)
Verfasst: Mi 26. Nov 2008, 12:55
von Thomas
in der übung am freitag ham wir das auch gemacht, haben dann aber nur daraus gefolgert, dass an nicht absolut konvergent ist. ich denk ma wenn dann leibniz auch nicht geht, heißt es dass die folge divergent is oder findet jemand noch ne andere möglichkeit?
Re: Aufgabe 20 (K)
Verfasst: Mi 26. Nov 2008, 13:26
von riQ
Ich hab
a) div (Quot.)
b) abs konv (Quot.)
c) abs konv (Quot.)
d) abs konv (Qout.)
e) ?
f) ?
g) alpha <1 => Reihe konv, alpha = 1 , an -> e => Reihe div, alpha > 1 => Reihe div (Wurzelkrit)
h) div (Min.)
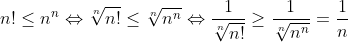
Re: Aufgabe 20 (K)
Verfasst: Mi 26. Nov 2008, 13:59
von Sascha
Re: Aufgabe 20 (K)
Verfasst: Mi 26. Nov 2008, 14:11
von riQ
falsch, du weißt schon, dass n^n was anderes ist als n^2 ...
Re: Aufgabe 20 (K)
Verfasst: Mi 26. Nov 2008, 21:11
von NebuK
Re: Aufgabe 20 (K)
Verfasst: Mi 26. Nov 2008, 21:39
von Rob
Ich bin zwar nicht deutsch, aber ich glaube, das sollte
Wider-Widerspruch heißen

OnTopic:
Kann mir bitte jemanden einen Lösungsansatz geben für g) und h)? Ich komme keinen Meter voraus... Keine Ahnung wie ich hier überhaupt anfangen muss... Alle andere Aufgaben habe ich schon gelöst

Re: Aufgabe 20 (K)
Verfasst: Mi 26. Nov 2008, 21:54
von riQ
Rob hat geschrieben:
Ich bin zwar nicht deutsch, aber ich glaube, das sollte
Wider-Widerspruch heißen

OnTopic:
Kann mir bitte jemanden einen Lösungsansatz geben für g) und h)? Ich komme keinen Meter voraus... Keine Ahnung wie ich hier überhaupt anfangen muss... Alle andere Aufgaben habe ich schon gelöst

g) Wurzelkrit. h) schau dir mal a_n an: Nullfolge?
Re: Aufgabe 20 (K)
Verfasst: Mi 26. Nov 2008, 22:15
von mocha
pedobear hat geschrieben:gleich am anfang ziehst du den betrag von an und machst den Bruch dann größer, am ende sagste dann yo und wegen minoranten etc...
das Minorantenkriterium besagt aber das wenn 0 <= bn <= an , nich wenn 0 <= bn <= |an|.
durch den betrag "klappste" ja einfach alle glieder über die x Achse un sagst dann yo das divergiert.
da aber eigentlich manche Glieder unter der x Achse sind, ist die summe von an ja westenlich kleiner als die von |an|, in dem Fall so stark das das an evtl nicht mehr divergiert !
nimm dir z.bsp. an= (-1)^n * 1/n
|an| = 1/n, das divergiert ja an sich.
so jetz lass die betragstriche weg... zackbumm nix mehr mit divergenz, alle glieder von sn sind kleiner gleich 1 :/
eine reihe konvergiert absolut, wenn ihr betrag konvergiert, deswegen hab ich am anfang den betrag genommen, ob sie überhaupt konvergiert kann ich so nicht feststellen, das hab ich mit leibnitz gemacht
Re: Aufgabe 20 (K)
Verfasst: Do 27. Nov 2008, 02:49
von Johann
Für die e) hab ich folgenden Ansatz benutzt: Wenn eine Reihe über eine Folge a_n konvergiert, so gilt lim a_n = 0. D.h. aber auch, dass wenn eine Folge nicht gegen 0 konvergiert, die Reihe über die Folge nicht konvergent sein kann. Im Falle der e) haben wir einen alternierenden Faktor mit einem Faktor, der gegen 1 geht. Demnach ist die Folge ja divergent, die Reihe darüber folglich auch.
Bei der f) haben wir einen alternierenden Faktor mit einem Faktor, der gegen 0 geht (sagt der TR, muss noch schauen wie ich das von Hand zeige), wonach das Leibnitz-Kriterium greift und man konvergenz (nicht aber abs. konvergenz!) gezeigt hätte.
Edit:
Zur g) habe ich ganz einfach das Wurzelkriterium angewendet. Wenn alpha keine Konstante ist (z.B. alpha = n), dann divergiert die Reihe. Ist alpha > 1 divergiert die Reihe nach dem Wurzelkriterium (das alpha ist gerade das limsup!), ist alpha < 1 konvergiert sie.
Zur h) habe ich herausgefunden, dass die Reihe divergiert. Mit dem Minorantenkriterium lässt sich das zeigen. Als Referenzreihe nehme man die harmonische Reihe. Die Folge 1/n ist wie durch Umformungen leicht zu zeigen ist kleiner als die Folge der gegebenen Reihe. Die harmonische Reihe divergiert aber, nach dem Minorantenkriterium die Reihe der h) dann aber auch.
ist doch größer gleich
nicht absolut konvergent
divergiert und damit auch