Aufgabe 20 (K)
- Kubik-Rubik
- Administrator
- Beiträge: 267
- Registriert: Di 21. Okt 2008, 19:55
- Wohnort: Kehl / Karlsruhe
Aufgabe 20 (K)
Hier kommen Fragen und Antworten zur 20. Aufgabe rein!
Registrierung nur noch mit E-Mail Adresse der Universität Karlsruhe möglich.
Mehr Informationen: Registrierung nur noch mit E-Mail Adresse der Universität
Notation für Übungsblätter - FACH[x]#y (Blatt x - Aufgabe y für FACH)
Mehr Informationen: Registrierung nur noch mit E-Mail Adresse der Universität
Notation für Übungsblätter - FACH[x]#y (Blatt x - Aufgabe y für FACH)
Re: Aufgabe 20 (K)
Hier ein, zur 20a) sehr ähnliches, Musterlösungsbeispiel in dem das Quotientenkriterium verwendet wird:
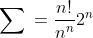
!2^{n+1}n^{n}}{n!2^{n}(n+1)^{n+1}} = \frac{2}{(1+\frac{1}{n})^{n}} \rightarrow \frac{2}{e} < 1)
Re: Aufgabe 20 (K)
a: divergent (quotientenkrit)
b: konvergent (maj)
c: abs konv (quotientenkrit)
d: abs konv (quotientenkrit)
e: divergent (leib)
f: abs konv (leib)
g: wenn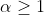 divergent (da fuer
divergent (da fuer 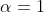 Reihe
Reihe 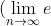 m fuer
m fuer 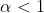 abs konv (wurzelkrit)
abs konv (wurzelkrit)
stimmen die ergebnisse mit euren ueberein?
wie seid ihr an die h rangegangen
gruss mark
b: konvergent (maj)
c: abs konv (quotientenkrit)
d: abs konv (quotientenkrit)
e: divergent (leib)
f: abs konv (leib)
g: wenn
stimmen die ergebnisse mit euren ueberein?
wie seid ihr an die h rangegangen
gruss mark
Re: Aufgabe 20 (K)
Mark, VORSICHT!
Das Leibniz-Kriterium sagt NICHT aus, ob eine Reihe divergent ist. (Tutorium, evtl. auch Übung und VL)
Das Leibniz-Kriterium sagt dir nur in bestimmten Fällen, dass deine Reihe konvergiert! Und es sagt NICHT aus, dass eine Reihe absolut konvergiert!
mfG
Markus
Das Leibniz-Kriterium sagt NICHT aus, ob eine Reihe divergent ist. (Tutorium, evtl. auch Übung und VL)
Das Leibniz-Kriterium sagt dir nur in bestimmten Fällen, dass deine Reihe konvergiert! Und es sagt NICHT aus, dass eine Reihe absolut konvergiert!
mfG
Markus
-
Christian S.
- Beiträge: 225
- Registriert: Sa 25. Okt 2008, 12:48
Re: Aufgabe 20 (K)
e konv. bei mir nach dem Wurzelkriterium, da die nte Wurzel von an < nte-Wurzel(sqrt(n) / sqrt (n)) = 1. Daraus folgt ja, dass der lim von der nten Wurzel von an < 1, wonach die Reihe doch nach dem Wurzelkrit. konvergieren müsste. Meinungen?
-
BenTreeser
- Beiträge: 42
- Registriert: Fr 24. Okt 2008, 15:35
- Wohnort: Karlsruhe
- Kontaktdaten:
Re: Aufgabe 20 (K)
ich hab die gleichen ergebnisse. Bloß:fuku hat geschrieben:a: divergent (quotientenkrit)
b: konvergent (maj)
c: abs konv (quotientenkrit)
d: abs konv (quotientenkrit)
e: divergent (leib)
f: abs konv (leib)
g: wenndivergent (da fuer
Reihe
m fuer
abs konv (wurzelkrit)
stimmen die ergebnisse mit euren ueberein?
wie seid ihr an die h rangegangen
gruss mark
- g) bin ich mir noch nicht sicher.
- h) habe ich ebenfalls abs. Konvergenz (Wurzelkrit).
- b) konv. (2. bin. Formel)
Zuletzt geändert von BenTreeser am Di 25. Nov 2008, 14:16, insgesamt 1-mal geändert.
Re: Aufgabe 20 (K)
Hm...Bei mir:
a) abs. konv. (Wurzel)
b) abs. konv. (Major)
c) abs. konv. (Wurzel)
d) divergent (Quot.)
e) nicht abs. konv., erfüllt Leibniz nicht => divergent (?)
f) abs. konv. (|an| gegen 0)
g) abs. konv. für a < 1, divergent für a >= 1 (Wurzel)
h) divergent (|an| gegen 1)
Bin mir bei allen auser e) recht sicher...
EDIT:
a) abs. konv. (Wurzel)
b) abs. konv. (Major)
c) abs. konv. (Wurzel)
d) divergent (Quot.)
e) nicht abs. konv., erfüllt Leibniz nicht => divergent (?)
f) abs. konv. (|an| gegen 0)
g) abs. konv. für a < 1, divergent für a >= 1 (Wurzel)
h) divergent (|an| gegen 1)
Bin mir bei allen auser e) recht sicher...
EDIT:
Das muss <= sein, und hier fallen die Grenzwerte zusammen. n-te Wurzel(c) geht gegen 1 für alle c>0 (Beispiel 2.21 im inoffiziellen Script, Satz 2.8 bei uns)Christian S. hat geschrieben:e konv. bei mir nach dem Wurzelkriterium, da die nte Wurzel von an < nte-Wurzel(sqrt(n) / sqrt (n)) = 1. Daraus folgt ja, dass der lim von der nten Wurzel von an < 1, wonach die Reihe doch nach dem Wurzelkrit. konvergieren müsste. Meinungen?
Zuletzt geändert von Ruben am Di 25. Nov 2008, 14:26, insgesamt 1-mal geändert.
Für Rechenfehler, Schreibfehler, Denkfehler oder sonstigen Dumfug wird keine Haftung übernommen!
-
BenTreeser
- Beiträge: 42
- Registriert: Fr 24. Okt 2008, 15:35
- Wohnort: Karlsruhe
- Kontaktdaten:
Re: Aufgabe 20 (K)
Bei der a) kommt 5/e > 1 --> divergent raus. Oder irre ich mich?Ruben hat geschrieben:Hm...Bei mir:
a) abs. konv. (Wurzel)
.
.
.
Bin mir bei allen auser e) recht sicher...
Re: Aufgabe 20 (K)
Also wenn man alles zusammenkürzt komm ich auf: 5/n * n-te wurzel(n!). Die Wurzel geht gegen 1 (siehe EDIT eins drüber) und 5/n gegen 0 -> Grenzwert ist 0
EDIT: Hm...n-te Wurzel gilt für c konstant...ich muss nochmal drüber meditiern...
EDIT: Hm...n-te Wurzel gilt für c konstant...ich muss nochmal drüber meditiern...
Für Rechenfehler, Schreibfehler, Denkfehler oder sonstigen Dumfug wird keine Haftung übernommen!
-
Thomas
- Administrator
- Beiträge: 383
- Registriert: Do 23. Okt 2008, 20:16
- Wohnort: Karlsruhe
- Kontaktdaten:
Re: Aufgabe 20 (K)
nimm dass quotientenkrit. dann kommt was gescheites raus