2. Übungsblatt - Abgabe 3. November
- Kubik-Rubik
- Administrator
- Beiträge: 267
- Registriert: Di 21. Okt 2008, 19:55
- Wohnort: Kehl / Karlsruhe
2. Übungsblatt - Abgabe 3. November
2. Übungsblatt
Abgabe: Einwurf der Lösungen bis zum 03.11.2008, 13:00 Uhr, in einen der Briefkästen im dritten Stock des
Mathematik-Gebäudes 20.30 neben dem Seminarraum S32.
Download:
2. Übungsblatt (Rechtsklick / Speichern unter...)
Fragen und Antworten kommen in diesen Thread rein!
Abgabe: Einwurf der Lösungen bis zum 03.11.2008, 13:00 Uhr, in einen der Briefkästen im dritten Stock des
Mathematik-Gebäudes 20.30 neben dem Seminarraum S32.
Download:
2. Übungsblatt (Rechtsklick / Speichern unter...)
Fragen und Antworten kommen in diesen Thread rein!
Registrierung nur noch mit E-Mail Adresse der Universität Karlsruhe möglich.
Mehr Informationen: Registrierung nur noch mit E-Mail Adresse der Universität
Notation für Übungsblätter - FACH[x]#y (Blatt x - Aufgabe y für FACH)
Mehr Informationen: Registrierung nur noch mit E-Mail Adresse der Universität
Notation für Übungsblätter - FACH[x]#y (Blatt x - Aufgabe y für FACH)
Re: 2. Übungsblatt - Abgabe 3. November
moin,
sachmal weiß einer von euch was man bei Aufgabe 1 machen soll??
ich hab mal "Gaußsche Normalform" gegoogled, aber nix ordentliches gefunden.
Wie bildet man sowas von einer Matrix?
MfG,
Patrick
sachmal weiß einer von euch was man bei Aufgabe 1 machen soll??
ich hab mal "Gaußsche Normalform" gegoogled, aber nix ordentliches gefunden.
Wie bildet man sowas von einer Matrix?
MfG,
Patrick
Re: 2. Übungsblatt - Abgabe 3. November
Moin,
da kann ich dir helfen. DIe Gaußsche Normalform ist einfach das, was wir in der vorletzten VOrlesung (glaube ich) gemacht hatten. Also einfach versuchen ein Dreieck mit '0'-en zu erreichen, so dass man die Werte für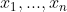 fast schon direkt ablesen kann. Funktioniert allerdings bei den gegebenen nicht wirklich gut.
fast schon direkt ablesen kann. Funktioniert allerdings bei den gegebenen nicht wirklich gut.
Sollte danach in einer ähnlichen Form sein (nicht die geg. Matrix):
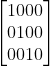
da kann ich dir helfen. DIe Gaußsche Normalform ist einfach das, was wir in der vorletzten VOrlesung (glaube ich) gemacht hatten. Also einfach versuchen ein Dreieck mit '0'-en zu erreichen, so dass man die Werte für
Sollte danach in einer ähnlichen Form sein (nicht die geg. Matrix):
Re: 2. Übungsblatt - Abgabe 3. November
|silent hat geschrieben:Moin,
da kann ich dir helfen. DIe Gaußsche Normalform ist einfach das, was wir in der vorletzten VOrlesung (glaube ich) gemacht hatten. Also einfach versuchen ein Dreieck mit '0'-en zu erreichen, so dass man die Werte fürfast schon direkt ablesen kann. Funktioniert allerdings bei den gegebenen nicht wirklich gut.
Sollte danach in einer ähnlichen Form sein (nicht die geg. Matrix):
Sicher?
Dachte sieht so aus:
1 0 0
y 1 0
x z 1
Naja wie dem auch sei; ich komm auch einfach net drauf, wie das gehn soll?
bei der A sind ja alle 3 Gleichungen gleich (einmal einfach das Doppelte und einmal *-1) komm immer nur auf
1 2 -1
0 0 0
0 0 0
Re: 2. Übungsblatt - Abgabe 3. November
Flow hat geschrieben:
Sicher?
Dachte sieht so aus:
1 0 0
y 1 0
x z 1
Naja wie dem auch sei; ich komm auch einfach net drauf, wie das gehn soll?
bei der A sind ja alle 3 Gleichungen gleich (einmal einfach das Doppelte und einmal *-1) komm immer nur auf
1 2 -1
0 0 0
0 0 0
hatte das gleiche problem und hab deswegen mal den tutor gefragt
er meinte
ist eine gaußsche normalform
nur wenn du in einer zeile eine eins hast und links davon nur nullen, dürfen über und unter der eins auch nur nullen stehen, zb
ist nur gauß-normal-dings wenn y == 0
Re: 2. Übungsblatt - Abgabe 3. November
Moinmoin,
Ich komm auch nur auf
1 2 -1
0 0 0
0 0 0
Allerdings hat Maple mir das selbe ausgespuckt, ganz so falsch kanns also nicht sein (naja ... man koennte total falsch gedacht haben..).
Wo ich mich eher Wunder ist bei der Nr. 2 (a). Ich krieg da in der letzten Zeile immer 0 0 0 = 4 raus, egal was ich mach. Gibts fuer die angegebenen Bs also keine Loesung? Dann waere die (b) ja reichlich einfach ;P. Komisch hier, auch auf das LGS hab ich mal Maple losgelassen:
Also ist wohl tat und saechlich 0 = 4? Oder was ueberseh ich hier?
Waer super wenn jemand ne Idee hat ;P.
Danke schonmal im Vorraus, Gruesse!
Ich komm auch nur auf
1 2 -1
0 0 0
0 0 0
Allerdings hat Maple mir das selbe ausgespuckt, ganz so falsch kanns also nicht sein (naja ... man koennte total falsch gedacht haben..).
Wo ich mich eher Wunder ist bei der Nr. 2 (a). Ich krieg da in der letzten Zeile immer 0 0 0 = 4 raus, egal was ich mach. Gibts fuer die angegebenen Bs also keine Loesung? Dann waere die (b) ja reichlich einfach ;P. Komisch hier, auch auf das LGS hab ich mal Maple losgelassen:
Code: Alles auswählen
[1 1 2 2]
[ ]
[0 -2 -2 -2]
[ ]
[0 0 -1 0]
[ ]
[0 0 0 4]
Waer super wenn jemand ne Idee hat ;P.
Danke schonmal im Vorraus, Gruesse!
Re: 2. Übungsblatt - Abgabe 3. November
Hab das Ding noch nich' gerechnet, aber vom Anschauen sieht man ja gleich:
Aufgabe 1
1. ...dass die 3 Gleichungen Vielfache von einander sind. Sprich als Normalform schreibt man einfach eine der Gleichungen in die erste Zeile und für die anderen beiden 0=0 (wie schon gesagt wurde)
2. ...dass es keine Lösung gibt. Ich komm da aber nicht auf 0=4, sondern
Aufgabe 1
1. ...dass die 3 Gleichungen Vielfache von einander sind. Sprich als Normalform schreibt man einfach eine der Gleichungen in die erste Zeile und für die anderen beiden 0=0 (wie schon gesagt wurde)
2. ...dass es keine Lösung gibt. Ich komm da aber nicht auf 0=4, sondern
Code: Alles auswählen
[1, 2, 2]
[0, 0, -1]
[0, 0, 0]
Cheers André
Re: 2. Übungsblatt - Abgabe 3. November
0 0 0 = 4 krieg ich bei der Nr. 2 raus, nicht Nr 1. ist ja von der zweiten von Nr. Eins....
Code: Alles auswählen
[1, 2, 2],[0,0,1],[0,0,0]Re: 2. Übungsblatt - Abgabe 3. November
setz bei der 2a) deine bs ein un probier x1=-5/2, x2=-1/2 und x3=4... alle gleichungen sind erfüllt 
also rechenfehler irgendwo
evtl zeile 3: die heißt 2 0 1 -1
das x1 is in der aufgabenstellung komisch eingerückt, den fehler haben wir erst gemacht
also hast dann
1 1 1 1
1 -1 1 2
2 0 1 -1
0 2 2 7
als matrix pew !
also rechenfehler irgendwo
evtl zeile 3: die heißt 2 0 1 -1
das x1 is in der aufgabenstellung komisch eingerückt, den fehler haben wir erst gemacht
also hast dann
1 1 1 1
1 -1 1 2
2 0 1 -1
0 2 2 7
als matrix pew !
I HAS FREE CANDYZ
Re: 2. Übungsblatt - Abgabe 3. November
Ich werde in diesem Post die Lösungen zu diesem Aufgabenblatt sammeln und IHR könnt' dabei helfen 
Lösung 1:
(I)

(II)

Lösung 2:
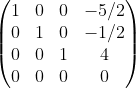
Lösung 3:
b)
A: Übungsblätter
B: Studenten (Personen)
Z(a,b): Zufrieden (wahr/falsch)
Va€A -]b€B: !Z(a,b) => -]a€A Vb€B: Z(a,b) //Negation
a) !-]a€A Vb€B: Z(a,b)
b) -]=1b€B Va€A: Z(a,b)
c) -]=1a€A Vb€B: Z(a,b)
d) Vb€B Va€A: Z(a,b)
e) Va€A !-]b€B: !Z(a,b)
! => Negation
-]=1 => "es existiert genau 1"
=> Neg. aus b) (sprich: -]a€A Vb€B: Z(a,b)) ist äquivalent zu c)
Lösung 1:
(I)
(II)
Lösung 2:
Lösung 3:
b)
A: Übungsblätter
B: Studenten (Personen)
Z(a,b): Zufrieden (wahr/falsch)
Va€A -]b€B: !Z(a,b) => -]a€A Vb€B: Z(a,b) //Negation
a) !-]a€A Vb€B: Z(a,b)
b) -]=1b€B Va€A: Z(a,b)
c) -]=1a€A Vb€B: Z(a,b)
d) Vb€B Va€A: Z(a,b)
e) Va€A !-]b€B: !Z(a,b)
! => Negation
-]=1 => "es existiert genau 1"
=> Neg. aus b) (sprich: -]a€A Vb€B: Z(a,b)) ist äquivalent zu c)
Zuletzt geändert von |silent am Mo 3. Nov 2008, 01:34, insgesamt 3-mal geändert.